动态规划——最大公共子序列

【问题描述】

字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。
给定两个字符序列A和B，如果字符序列Z既是A的子序列，又是B的子序列，则称序列Z是A和B的公共子序列。该问题是求两序列A和B的最长公共子序列（LCS）。

【问题分析】

b[i][j]为子序列（x0，x1，…，xi-1）和（y0，y1，…，yj-1）的最长公共子序列的长度。

【解决思路】

引进一个二维数组c[][]，用c[i][j]记录X[i]与Y[j] 的LCS 的长度，b[i][j]记录c[i][j]是通过哪一个子问题的值求得的，以决定搜索的方向。
我们是自底向上进行递推计算，那么在计算c[i,j]之前，c[i-1][j-1]，c[i-1][j]与c[i][j-1]均已计算出来。此时我们根据X[i] = Y[j]还是X[i] != Y[j]，就可以计算出c[i][j]。
递归方程为：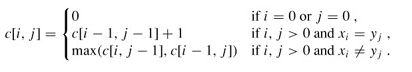
回溯输出最长公共子序列过程：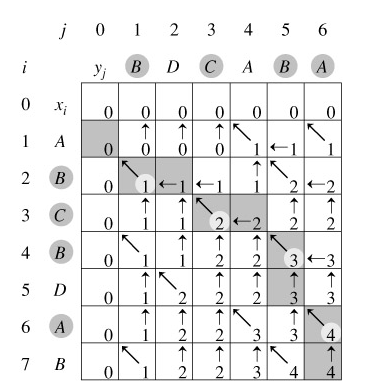

【代码实现】

#include <stdio.h>
#include <string.h>
#define N 100
void LCSLength(char *x, char *y, int m, int n, int c[][N], int b[][N])
{
    int i, j;
    for(i = 0; i <= m; i++) c[i][0] = 0;
    for(j = 1; j <= n; j++) c[0][j] = 0;
    for(i = 1; i<= m; i++)
    {
        for(j = 1; j <= n; j++)
        {
            if(x[i-1] == y[j-1]){
                c[i][j] = c[i-1][j-1] + 1;
                b[i][j] = 0;
            }
            else if(c[i-1][j] >= c[i][j-1]){
                c[i][j] = c[i-1][j];
                b[i][j] = 1;
            }
            else{
                c[i][j] = c[i][j-1];
                b[i][j] = -1;
            }
        }
    }
}
void PrintLCS(int b[][N], char *x, int i, int j)
{
    if(i == 0 || j == 0)
    return;
    if(b[i][j] == 0){
        PrintLCS(b, x, i-1, j-1);
        printf("%c ", x[i-1]);
    }
    else if(b[i][j] == 1)
    PrintLCS(b, x, i-1, j);
    else
    PrintLCS(b, x, i, j-1);
}
int main()
{
    char x[N],y[N];
    //char x[N] = {"ABCBDAB"};
    //char y[N] = {"BDCABA"};
    printf("分别输入字符序列x和y：\n");
    scanf("%s",&x);
    scanf("%s",&y);
    int b[N][N];
    int c[N][N];
    int m, n;
    m = strlen(x);
    n = strlen(y);
    LCSLength(x, y, m, n, c, b);
    printf("最大公共子序列为：\n");
    PrintLCS(b, x, m, n);
    return 0;
}

【运行结果】

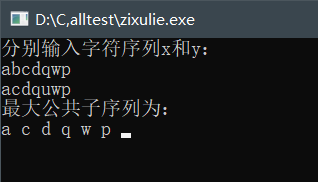
运行结果仅供参考