【问题描述】
有如下图所示的一个数塔,从顶部出发,在每一结点可以选择向左走或是向右走,一直走到底层,要求找出一条路径,使路径上的数值和最大。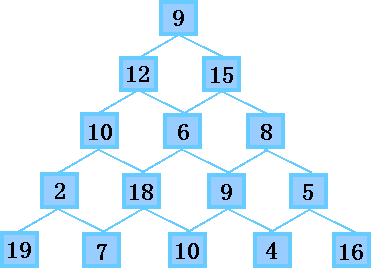
【问题分析】
有一个r行的数塔,数塔上有若干数字。问从数塔的最高点到底部,在所有的路径中,经过的数字的和最大为多少?
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16如上图,是一个5行的数塔,其中9—12—10—18—10的路径经过数字和最大,为59。
1.2 解法思路
面对数塔问题,使用贪心算法显然是行不通的,比如给的样例,如果使用贪心算法,那选择的路径应当是7—8—1—7—5,其经过数字和只有28,并不是最大。而用深搜DFS很容易算出时间复杂度为 O2^n (因为每个数字都有向左下和右下两种选择),行数一多必定超时。
所以,数塔问题需要使用动态规划算法。
我们可以从上往下遍历。
可以发现,要想经过一个数字,只能从左上角或右上角的数字往下到达。
所以显然,经过任一数字A时,路径所经过的数字最大和——是这个数字A左上方的数字B以及右上方的数字C两个数字中,所能达到的数字最大和中较大的那一个,再加上该数字A。
故状态转移方程为: dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+num[i][j]
其中i,j表示行数和列数,dp表示储存的最大和,num表示位置上的数字。
dp[i-1][j] 表示左上角, dp[i-1][j-1] 表示右上角。
以样例来说明:在经过第三行的数字1时,我们先看它左上角的数字12和右上角的数字15其能达到的最大和。12显然只有9—12一条路径,故最大和是21;15显然也只有9—15一条路径,其最大和是24;两者中较大的是24,故经过6所能达到的最大和是24+6=30。
这样一步步向下遍历,最后经过每一个位置所能达到的最大和都求出来了,只要从最底下的一行里寻找最大值并输出即可。
我们也可以从下往上遍历。
一条路径不管是从上往下走还是从下往上走,其经过的数字和都是一样的,所以这题完全可以变成求——从最底层到最高点所经过的最大数字和。
其写法与顺序遍历是一样的,只是状态转移时,变成从该数字的左下角和右下角来取max了。逆序遍历的写法相比于顺序遍历优点在于:少了最后一步求最后一行max的过程,可以直接输出最高点所储存的值。
【代码实现】
#include <stdio.h>
int num[100][100];//用于储存数塔每个位置的数字
int dp[100][100];//用于储存经过数塔每个位置所能达到的最大和
int max(int a,int b)
{
return a>b?a:b;
}
int main()
{
int r;
printf("输入数塔行数:");
scanf("%d",&r);//输入数塔行数
printf("输入数塔数据:\n");
for(int i=1;i<=r;i++)
for(int j=1;j<=i;j++)
scanf("%d",&num[i][j]);//输入数塔数据,注意i和j要从1开始,防止数组越界
for(int i=1;i<=r;i++)//共计r行
for(int j=1;j<=i;j++)//每行有j个数字
dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+num[i][j];
//经过该数字的最大和,为左上角和右上角中的max,再加上该数字
int ans=0;
for(int i=1;i<=r;i++)
ans=max(ans,dp[r][i]);//从最后一行中找到最大数
printf("数塔路径和值最大为:%d\n",ans);//就是答案
return 0;
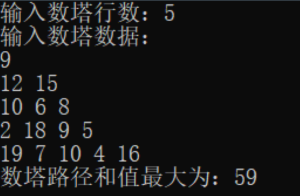
}【运行结果】
运行结果仅供参考
可以留下你的信息哦(去Github_issues)😀😀😀
GitHub Issues